Download the PDF file

References 

AR 70-38, Research, Development, Test and Evaluation of Materiel for Extreme Climatic Conditions, 1 Aug 79 

MIL-STD-210, Climatic Extremes for Military Equipment, 15 December 1973 

MIL-STD-810, Test Method Standard for Environmental Engineering Considerations and Laboratory Tests, 14 July 1989 

EIA Engineering Bulletin SSB-1, Guidelines for Using Plastic Encapsulated Microcircuits and Semiconductors in Military, Aerospace, and Other Rugged Environments

Background 

To determine the reliability of equipment requires knowledge of the stresses that the item will endure during its lifetime.  The stresses include natural environments (such as ambient temperature and humidity, solar radiation, atmospheric radiation, atmospheric pressure), induced environments (such as vibration on vehicle, handling drop shock, power dissipation heating, chemical exposure), and operational duty cycle.  Army Regulation AR 70-38 and MIL-STD-210 define world-wide climactic extremes as well as typical environmental conditions.  MIL-STD-810 also addresses the natural environments in addition to induced environments.  A valid equipment system specification will include the requirements for environments, duty cycle, reliability, and useful life; however, often the system specification will not provide specific life cycle environment profiles.  The qualification requirements for the system should address the anticipated life cycle exposure, such as that represented in Figure 1 , but due to the complexity of a system and the asset value, the reliability verification requires additional data from lower level testing on sub-assemblies, components, and parts, so that the stresses experienced by these elements requires characterization.

 

 

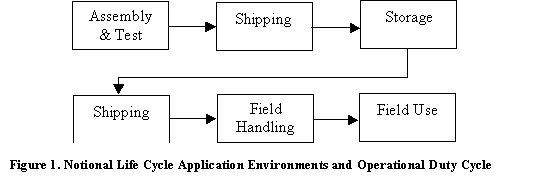
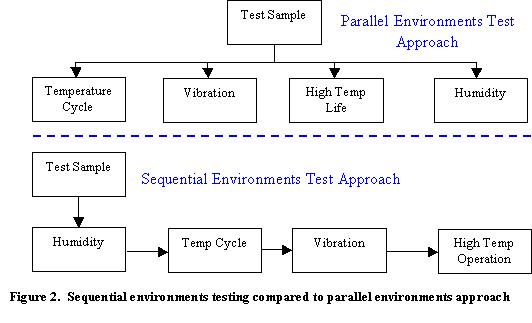
Figure 2 presents two common qualification test approaches applied at any particular assembly level.  The sequential environments approach provides the best method of assessing the effects of life cycle stresses, since it addresses cumulative degradation from the various environments and operating conditions, as well as the potential synergies that amplify the effect of a particular environment due to exposure to a previous environment.  The parallel test approach cannot evaluate these synergistic effects, since it does not expose the product to multiple environments.

Approach

The development of qualification requirements for a part necessitates the understanding and documentation of the anticipated life cycle environmental exposure and operational duty cycle.  Figure 1 depicts a generic typical life cycle scenario for a product.  Each of the life cycle elements includes environmental stresses and operational duty cycles that will consume some of the useful life of the item.  Some of these environments induce synergistic effects, so that the order and combination of stresses becomes important in overall effect on the product.  These system level stresses will induce possibly attenuated or amplified stresses at the part level.  For instance, solar radiation and power dissipation can elevate part temperatures far above the ambient temperature of the system, yet the thermal mass of the system can attenuate temperature changes. 

Qualification requirements for a part will typically include accelerated stress tests, since the application requirements will specify lifetimes in excess of practical test times.  The use of accelerated test conditions then require the use of degradation mechanism models to correlate such conditions to actual use conditions.  To address the sequential and simultaneous stresses, the qualification requirements must reflect the synergies of the various degradation mechanisms by judicious ordering and combining of stresses.  The application of degradation models must address the range of possible degradation mechanisms and associated model parameters to develop test times that can detect degradation mechanisms with low acceleration factors.  By proper ordering of sequential environments, the superposition of the degradation effects can approximate the actual use conditions.  EIA SSB-1 provides a comprehensive summary of failure mechanisms that apply to plastic encapsulated microcircuits (and can be extended to some other part and package types) along with discussion on applying superposition of stresses to evaluate life cycle reliability.  The models in SSB-1 do not address the degradation synergies of the various environments.

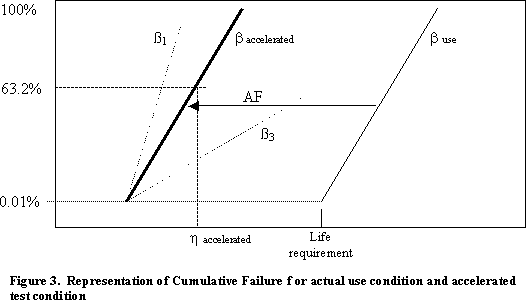
Figure 3 represents the cumulative failure distributions of the actual use and accelerated test conditions using the Weibull distribution, where a particular failure mechanism causes a cumulative failure distribution with Weibull slope, b actual, and 0.01% failing at the “life requirement.”  Under accelerated stress, the failure mechanism will cause a cumulative failure distribution shifted in time to result in 0.01% failure at an earlier time, t accelerated.  In general. the Weibull slope can be different between the accelerated and actual use conditions (such as ß₁ and ß₃), and only for the case where the use condition time, t_use, is proportional to the accelerated condition time, t_accel, (e.g., t_use = AF*t_accel, where AF is the acceleration factor) will the slopes will be equal.  A relatively generic transform of t_use = AF*(t_accel)ⁿ implies that buse =  baccel/n.  With a large sample size, a test can determine the time for a cumulative failure fraction of interest and then use the acceleration model transform to determine when that particular cumulative failure fraction will occur in actual use.  Sample size limitations often require assessment at a higher cumulative failure fraction.  In this case, assumptions about the Weibull slope transform will impact the acceptance criteria.  The existence of multiple failure mechanisms within a part with different acceleration factors under a particular stress further complicates the development of acceptance criteria for a sample test.  Figure 4 shows the influence of activation energy, E_a, assumptions on the acceleration factor for the Arrhenius model, t_failure = Ae^(Ea/kT), which provides an example of the importance in assessing both the range of applicable model parameters for a given failure mechanism (may depend on process control) and for accounting for competing failure mechanisms in a given part.  The final test requirements must account for all of these concerns along with the consumer and producer risks (i.e., the risk of accepting “bad” parts and the risk of rejecting “good” parts).

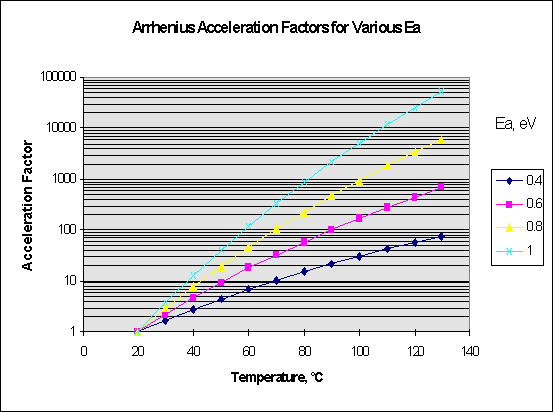
Figure 4.  Acceleration Factor dependence on activation energy for the Arrhenius reaction rate model, showing large sensitivity to activation energy assumptions

To determine appropriate test sample sizes requires consideration of the intended failure rate, and the failure distributions in both use and under accelerated conditions.  The simplest case involves mechanisms where the failure mechanisms have the same shape, and represents the common assumption where both situations result in an exponential (constant failure rate) distribution.  Consider a requirement that specifies less than 1% failure at t_life.  A sample size of 230 units with no failures would provide 90% confidence in meeting that requirement.  If test data on similar devices with the same failure mechanism exists to show that an accelerated test can provide acceleration, AF, a test time on these 230 units of t_life/AF will assure meeting the requirement.  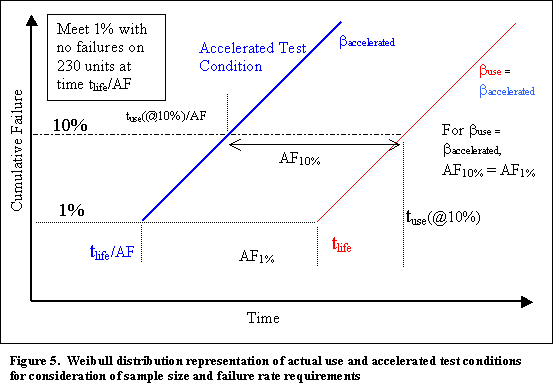The representation in Figure 5 suggests that increasing the test time can accommodate a smaller test sample, since longer test times allow sensitivity to larger cumulative failure quantities.  In this case, using 10% cumulative failures as the performance measure requires a longer test time, but fewer samples (i.e., a sample of 22 provides 90% confidence of fewer than 10% defective).  The uncertainty in the actual failure distribution poses the risk that this assumption will result in improper characterization of the 1% failure point of interest.  In addition, the general case with no similarity between the use and accelerated condition failure distributions (e.g., different b ’s for the Weibull distribution, see Figure 3) introduces uncertainty into the validity of the estimate that requires assessment in the test development rationale.

Failure mechanism models often only address the wear-out of properly assembled devices, and do not necessarily relate to devices constructed with inadequate process control or materials.  If the mainstream part capability greatly exceeds the projected life requirement, the test specification may require extension to verify the absence of process or material variations that cause early failures in a small portion of the part population.  For instance, evaluation of an application requirement may indicate that 100 temperature cycles over a wide range equates to the life cycle requirement, yet the general part qualification requirements include 500 temperature cycles. 

Summary

The qualification requirements should account for the life cycle environments and duty cycle, as well as the failure mechanism model parameter assumptions and the test sample size.  The approach described herein provides a generic approach for establishing qualification requirements for parts and assemblies.  Table 1 summarizes the step involved in developing the qualification requirements.